Визуальный язык ДРАКОН
Визуальный язык ДРАКОН
Дружелюбный Русский Алгоритмический язык, Который Обеспечивает Наглядность/Надёжность
Инструменты пользователя
Содержание
Упорядочение маршрутов: чем правее, тем... придумай сам
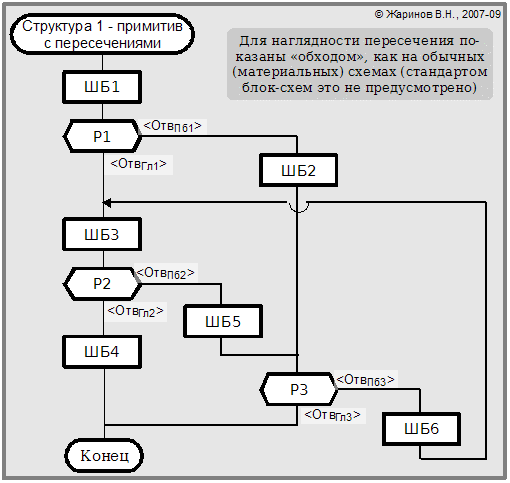
Принципы ШМ эргономически выгодно отличаются от принятого в блок-схемах порядка, при котором:
* выходы развилок (предикатных вершин) обычно направлены в разные стороны от оси входа;
- вход и выход вершин следования не требуется располагать на одной оси (а обычно даже их оси составляют прямой угол, т.е. вершина в то же время является точкой излома следования; часто это делают, чтобы «сэкономить» на звене вертикали перед/после излома);
- возможны наклонные линии связей, часто «ступеньки» на них, порой даже «обратное следование» - загиб вертикали против направления от начала к концу схемы.
Иногда такую организацию блок-схем называют «анархической». Она критикуется рядом авторов, скажем, Б. Мейером в "Почувствуй класс", Гл. 7.
По сути, в стандартах на БС и не существует чётких правил упорядочения элементов и подсхем. Тогда как ШМ, в общем-то, и есть система таких правил, только данная в математическом смысле не формально («что есть правильная схема»), а конструктивно («как построить правильную схему из правильной заготовки»).
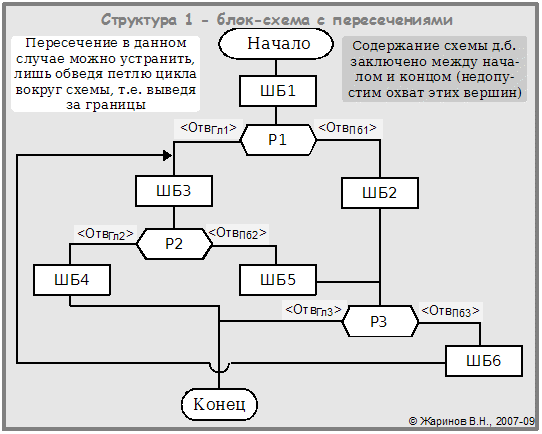
В сравнении с БС упорядоченность шампур-схемы можно видеть на рисунках ниже.
Шампур-схема закономерно асимметрична. Это даёт возможность показать упорядоченность маршрутов по какому-то критерию. Не всегда такой критерий нужно или можно определить по смыслу схемы; в этом случае порядок м.б. произвольным или введён по какому-то абстрактному правилу.
В то же время запрещение ступенек и загибов сужает возможности компоновки схемы в конкретном формате. Однако это можно понимать как плату за упорядоченность схемы.
Каким же образом в шампур-схемах уходят от «анархии»? Для этого и существуют нелинейные конструкции. Любую из них можно структурно подразделить на два типа частей:
- тела вертикалей — то, чем мы «нагрузили» составной атом (вложенные атомы, если мы рассматриваем матрёшку) — поэтому можно тела называть ещё нагрузкой;
- «каркас», остающийся, если мысленно отбросить нагрузку — будем называть его кроссом.
Какое-то тело может отсутствовать — тогда говорят, что эта вертикаль не нагружена. Атомы определены так, что все вертикали сразу нельзя оставлять без нагрузки. Т.е. в завершённой схеме не м.б. конструкции из одного только кросса — если понимать её как описание алгоритма, то это был бы т.н. пустой оператор.
В линейной схеме также можно условно выделить кросс — если отбросить все вершины, то останется цепочка звеньев вертикали; крайние сверху и снизу звенья одним своим концом будут присоединяться к заголовку и концу соответственно.
Развилки, циклы и инварианты
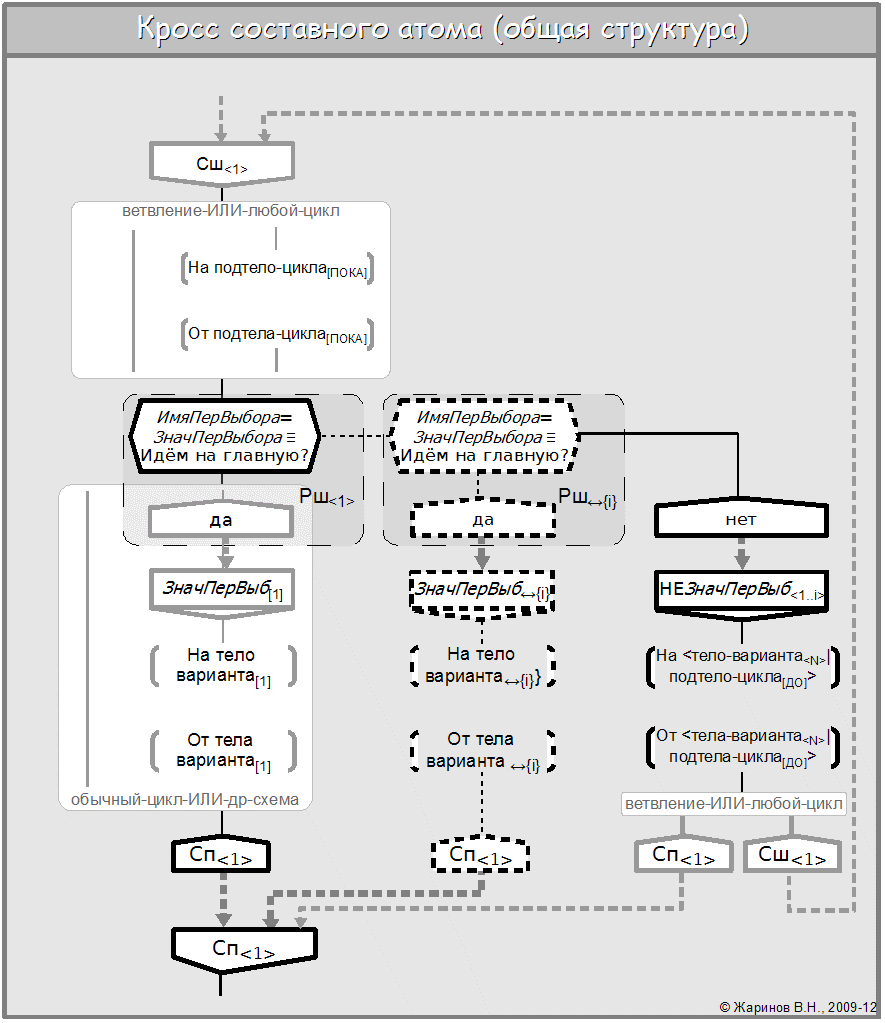
Рассмотрим кросс составного атома в общем виде — предполагая отбрасываемую нагрузку призвольной. Удобно показать его, как говорят, инвариантно — т.е. «для всего сразу», выделяя общее для всех разновидностей предметов и частное для тех или иных разновидностей. В данном случае мы совмещаем прежде всего переключатель и переключающий цикл:
В данном случае частное в инварианте представлено через графит-выбор подсхем по ИЛИ, а также подведением под РБНФ.
Верхняя схема построена из лексики техноязыка, как мы её дали ранее. Нетрудно выделить в кроссе верхнюю и нижнюю гребёнки и петлю цикла; здесь они напрямую не связаны -только через другие вершины или более крупные части конструкции. А что между ними и как всё это работает? Это можно понять, раскрывая смысл соединителей и разветвителей по образцу, также предложенному ранее. Что и сделано на нижней схеме.
Нетрудно видеть, что вершины Вариант — это просто именные части БП-контактов на выходах разветвителей верхней гребёнки. А адресные части вместе с логикой развилок мы не показываем на реальных схемах. Эргономически это правильно — позволяет сосредоточиться на значениях для выбора варианта. Если же показать, как здесь — то видно, что обычный цикл тоже можно получить из данной структуры. Надо только исключить при переходе к циклу и первый вариант переключателя, а также определение переменной выбора. Так у нас получится цикл ПОКА. Чтобы показать реализацию гибридного цикла (или цикла ДО), инвариант нужно дополнить, как показано на следующей схеме.
В текстовых ЯВУ обычно цикл ПОКА записывается через ключевые слова WHILE-DO-[W]END, а цикл ДО — через REPEAT-UNTIL.
На этих схемах мы снова пользуемся понятием позиции, введённым в первом разделе. Здесь «белый ящик» в некоторых позициях задаёт варианты подстановки части в схему. Причём мы не только помещаем варианты внутрь знака «белого ящика выбора» (области с текстом условия выбора — в данном случае по ИЛИ) — но иногда «подключаем» части к знаку позиции снаружи, выделяя их цветом и толщиной линии. Это удобно, если конфигурация частей сложна — тогда бы и «белый ящик» пришлось делать сложной формы, что неудобно. Интуитивно понятно, как найти конец позиции — он там, где начинается обычное оформление графики схемы.
В нашем случае вне позиций остаётся и часть схемы. А «белые ящики выбора» участвуют в определении инвариана. Как и до этого, частное в инварианте представлено также через графит-выбор подсхем по РБНФ.
Снова возвращаясь от синтаксиса к содержанию, видим разницу в том, что в обычном цикле не нужен и первый вариант переключателя. Можно сказать и иначе — в схеме на этом месте будет следующий шампур-блок, никакого отношения к рассматриваемой конструкции не имеющий.
Как видим, «подвал» составного атома (и конструкции на его базе) в любом случае имеет смысл кратных БП.
Обратим внимание — изломы возможны только в гребёнках. А направление следования по вертикалям везде одинаковое — от начала к концу схемы. Оно ещё называется «по шампуру». Только в петле цикла есть вертикаль, по которой следуют против шампура — для того эту петлю и определили как единицу лексики техноязыка.
А что будет, если убрать из схемы и первую развилку? В разветвлённом варианте останется шампур-блок (возможно, ограниченный с начала и с конца контактами-БП) — или просто звено вертикали. А в циклическом — либо также звено, либо два шампур-блока (подтела ДО и ПОКА), разделённых контактом, либо один из них. Причём всё это «зациклено» - т.е. раз войдя в полученную конструкцию, исполнитель будет постоянно проходить по ней — пока либо машину не выключить, либо — при наличии процесса-партнёра, способного управлять исполнением, — пока этот процесс не «снимет» зациклившийся.
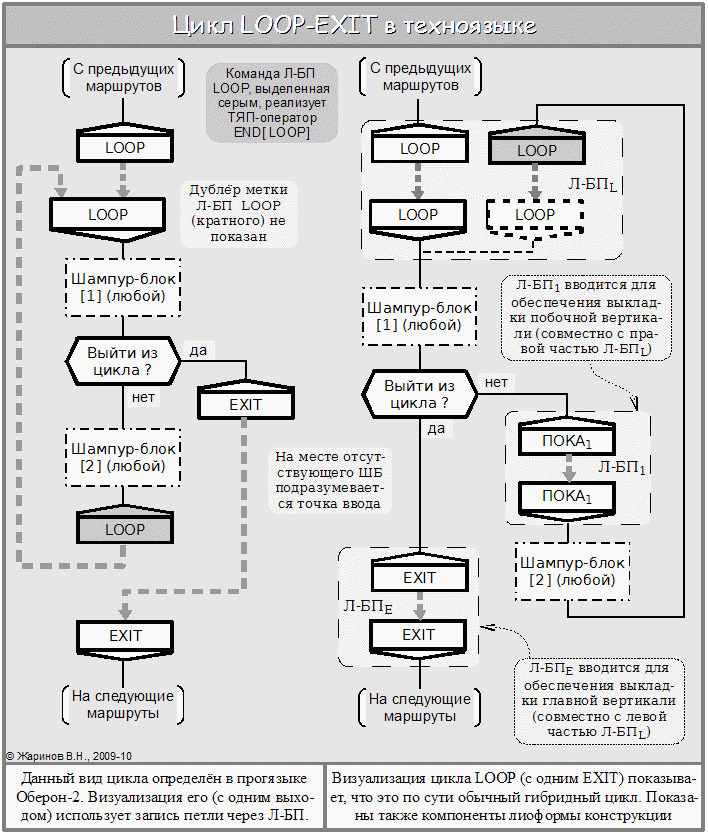
В алгоритмизации, однако, такое «зацикливание» м.б. и целесообразным. Часто тот же «первый среди равных» процессов-партнёров зацикливают — чтобы он управлял другими процессами с момента своего запуска до выключения машины. Поэтому и в языки программирования вводят иногда такой цикл в явном виде — т.н. конструкция LOOP-END. Чаще допускают выход из «зацикливания» - тогда получается конструкция LOOP-EXIT-END. Визуализировав её, можно видеть, что это обычный цикл:
Как видим, для этого достаточно сделать рокировку плеч EXIT-развилки.
Возможно и несколько выходов из цикла. Но при этом конструкция получается неструктурной, если не соблюдены некоторые ограничения на следование их развилок. Обсудим их в разделе о структурной алгоритмизации.
В текстовом виде цикл LOOP есть далеко не вовсех языках. Но можно его «эмулировать» - выразить через конструкции, имеющиеся в этих языках. Достаточно взять обычный цикл (гибридный, ПОКА, ДО) и записать его условие как заведомо истинное (можно просто записать константу логического типа со значением, соответствующим ответу «да»).
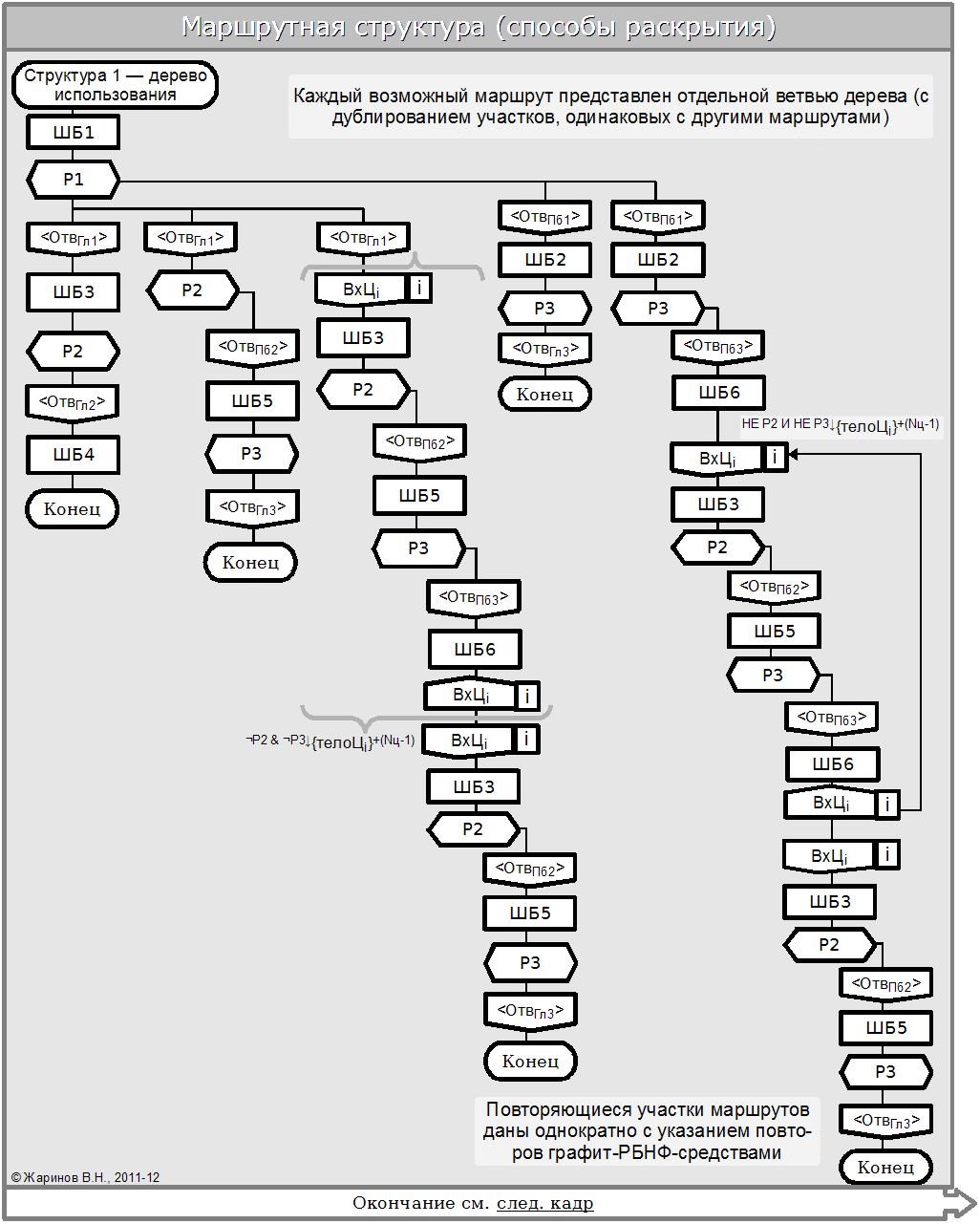
Варианты использования: разводим и сводим маршруты
Дракон-схема, как и БС, математически есть т.н. сводимый граф. Это значит, что у неё один конец, куда должны сойтись все маршруты, ведущие к нужному результату. Поэтому нужны и вершины-соединители маршрутов; на них мы останавливались здесь.
Разумеется, строгое определение графа как математического объекта не может исходить из смысла слова, которым его назвали - тем более обыденного… ![]() Поэтому укажем ещё на существенное именно для данного класса графов свойство:
Поэтому укажем ещё на существенное именно для данного класса графов свойство:
«Класс графов называется в теории графов аранжируемыми (в одной аксиоматике), сводимыми (в другой аксиоматике, у новосибирцев - Евстигнеева-Касьянова) и устремлёнными уже назван мной, с третьей стороны (по-третьему были введены; уже потом выяснилась эквивалентность этих классов). Проще всего объяснить так: направленный граф с выделенной начальной вершиной, в котором разрешаются только такие циклы, при которых каждая дуга может быть классифицирована либо как прямая, либо как обратная (обратная дуга при этом идёт в доминатор той вершины, из которой выходит). Совсем неформально можно сказать, что запрещается вход в середину цикла.» И. Е. Ермаков, веб-сообщение
Заметим, что можно и не сводить маршруты. Тогда схема нелинейного алгопроцесса будет деревом, у которого и главный, и каждый побочный маршруты имеют отдельный конец. Также и все цепочки, общие для разных маршрутов, дублируются. Циклы же разворачиваются — т.е. путь в цикле повторяется подряд столько раз, сколько итераций цикла (проходов по нему) будет при исполнении. Обычно заранее можно предсказать только максимальное и минимальное число итераций — так что и при описании развёрнутого цикла без РБНФ не обойтись.
Читать такую схему сложнее физически из-за большего объёма; но иногда она нагляднее показывает логику процесса. Кроме того, это промежуточное представление на пути к отдельному описанию каждого маршрута (которое часто возникает в ходе сочинения и допускается в формализации в виде т.н. вариантов использования — англ. use cases). Такой вариант — это конкретная реализация описания нелинейного процесса, его развёртка «рабочей точкой» (как ещё говорит Паронджанов, «дракон-поездом»).
Каждый вариант нелинейного процесса — это соответствующий маршрут, оформленный как линейная дракон-схема под общим именем процесса (возможно, с добавлением какого-то индекса маршрута для удобства различения). Представление его на техноязыке - любая дракон-схема с т.н. «хвостами» - неприсоединёнными побочными выходами развилок. Примером может служить схема на с. в «Занимательной информатике» Паронджанова:
Заметим, что в книге такая схема трактуется как логически ошибочная. Так и есть — если считать её завершённой, а не развёрткой отдельного маршрута. В то же время способ сочинения «визуалов с хвостами» нужно считать вполне естественным. В самом деле, часто сочинитель описывает реальную деятельность (или проектируемый процесс) отдельно по каждому пути от «дано» к «надо» - обычно начиная с более удобного или уже проверенного. Рассуждая примерно так: «сначала делаем то-то и то-то… тут надо, чтобы выполнилось это — а что будет, если не выполнилось — нас не интересует… потом делаем то-то и то-то… после чего должно иметь место это… » …ну и т.д. В дальнейшем появляются описания, как действовать, если что-то не выполняется — и у «хвостов» появляются продолжения. Постепенно (или сразу) «концы сводятся с концами» - определяется, какое продолжение ведёт к цели сразу (т.е. на конец всего алгоритма), какое должно «втекать» в одно из остальных (и в каком месте) — и дерево превращается в сводимый граф — т.е. в ту же дракон-схему. Которую, однако, можно снова и «развести» в дерево, и «расплести» на маршруты-представления вариантов использования…
В отношении синтаксиса уточним, что здесь правильно будет оформить ответы на вопросы развилки в вершинах Имя — как мы сделали при раскрытии соединителей и разветвителей ранее. Здесь такая вершина при побочном выходе будет обозначать начало маршрута, не входящего в вариант использования. Полезно будет и указывать присоединения таких маршрутов — тоже вершинами Имя.
В случае циклов на схеме маршрута будут «хвосты», ведущие вверх (против шампура) — от побочных выходов условий циклов. Вершина Адрес такого хвоста будет началом петли цикла. И нужно явно указывать конец петли (точку возврата) — также вершиной Имя выше по шампуру. Здесь следует использовать и поля индекса цикла.
А что делать, если есть «не сводимые» к нужному результату концы? Т.е. продолжения, возможные, но не ведущие к результату? При информатизации их оформляют как т.н. исключения - «побочные» выходы из процесса. Понятно, что надо иметь, куда выходить — значит, д.б. первичный процесс, где исключение можно обработать. Тем самым также возникает некая система дракон-схем (дракон-модель, обсуждавшаяся вкратце здесь). Первичный алгопроцесс в зависимости от организации бывает либо вызывающий (вышележащий вплоть до головного), либо «родительский» (базовый). Принцип исключений мы описывать не будем — читатель может найти в той же книге Кауфмана (Ч.I, Гл. 8). Если же исключение обработать негде/нечем — значит, система будет работать ненадёжно (может и создать проблемы).
Если даже маршруты полностью различны после какой-то развилки — всё равно в дракон-схеме надо их соединить — иначе она не будет сводимым графом. Соединитель тогда ставится прямо перед вершиной Конец.
А есть варианты использования у линейного алгопроцесса? Да, есть единственный вариант — совпадающий со структурой маршрутов всего процесса. В качестве примера можно снова привести схему из «Занимательной информатики»:
Заодно здесь можно увидеть понимание схемы как «железной дороги» для «дракон-поезда».
Направление движения — это и есть направление «по шампуру». А выделенная белым часть схемы — пример простого шампур-блока. В данном случае он охватывает всё тело схемы.
В качестве примера покажем представления маршрутов для схемы, уже рассматривавшейся ранее. Начнём с развёртки сводимого графа в дерево:
Здесь показаны разные возможности сокращённой развёртки цикла. В любом случае они используют РБНФ-итератор.
На основе дерева уже нетрудно составить разложение в набор вариантов использования:
Здесь мы представляем другие варианты оформления РБНФ-графит-подстановки на схеме. Это области различной формы как «ритмические полосы»:
- «габаритная» - прямоугольник, описанный около фрагмента схемы;
- «фигурная» - сохраняющая в заданных пределах отступы от габаритов содержания, своего рода «маленькое серое платье», следующее внешней форме фрагмента.
В данном случае мы сохраняем упорядочение побочных участков вправо. Поэтому более удобна фигурная область. Габаритная же легко накладывается, но удобна только при линейной компоновке содержания.
Текст итераторов содержит условие повторения тела, направление следования вхождений и запись диапазона повторов вхождения. Условие записано в двух вариантах: с русскоязычными названиями логфункций и международными, принятыми в ряде прогязыков.
Диапазон повторов указан по Б. Мейеру (со знаками регулярных выражений). В данном случае знак '+' указывает на начало числа повторений с единицы (т.к. по схеме у нас гибридный цикл, где тело выполнится хотя бы один раз). При выходе же из цикла выполнится только ПОКА-подтело; поэтому оно продублировано отдельно, а число повторов уменьшено на единицу в сравнении с предельным числом итераций цикла (Nц).
Ответы развилок мы оформили как ответные части БП-контактов, как уже делали ранее.
Отступление: варианты использования до нашей эры
Известна следующая притча о борьбе древних греков с персидскими завоевателями. Перед решающим сражением персидский военачальник прислал грекам письмо. Примерно следующее: «Если <случится то-то>, и <то-то>, и <то-то>… то мы победим.» Греки ответили кратко: «Если!». И выиграли битву.
Что можно сказать об императивном знании, заключённом в этих письмах? Персы, по сути, предложили вариант использования для предстоящего сражения. Но если взглянуть на него с учётом понимания естественного языка (русского в данном случае), то… можно видеть, что это вариант, понимаемый, так сказать, как «неглавный»… Если его визуализировать - то не как вертикаль, а как «лесенку», т.е. со связями каждый раз через побочный выход развилки. А «хвосты» будут от главных выходов каждой развилки. Можно сказать, что здесь выражено некое сомнение в успехе дела - т.е. предполагался исход, неблагоприятный для самих персов. А греки своим ответом выразили уверенность в таком же исходе - который для них, разумеется, полагается благоприятным.
Так что с помощью схем можно выражать не только суть дела, но и определённые аспекты отношения к нему. Думается, сочинителям полезно будет иметь это в виду.